Feeling tongue-tied trying to explain those tricky chicken-and-rabbit problems in math? You’re not alone! Many parents wonder why kids need to count animals from the number of legs. These seemingly impractical scenarios actually teach important math concepts and problem-solving skills.
In this article, our Spark Math teachers demystify these classic problems and show you why they’re valuable. Plus, we’ll share some easy methods and free practice worksheets, from primary to international competition levels, to help your young mathematician master them. Let’s turn those puzzled looks into ‘aha’ moments!
What are Chicken-and-Rabbit Problems?
Chicken-and-rabbit problems are math puzzles often used to teach problem-solving skills. They involve finding the number of chickens and rabbits based on the total number of animals and their legs.
| A farmer has 17 chickens and rabbits. He counts 52 legs in all. How many chickens and how many rabbits does he have? |
| Benny paid $45 in all for 12 pieces of five-dollar and two-dollar stamps. How many pieces of two-dollar stamps did he buy? How many pieces of five-dollar stamps did she buy? |
Chicken-and-rabbit problems are common in Singapore Mathematics, which emphasizes using math heuristics in problem-solving. These problems commonly appear in lower primary levels, as well as the national PSLE Math exam. They are also featured in international math contests, such as the International Junior Math Olympiad (IJMO) and AMC 8 for primary or middle-school students.
Why are Chicken-and-Rabbit Problems Important in Singapore Mathematics Education?
Chicken-and-Rabbit Problems teach important mathematical thinking and math heuristics, including:
- Drawing it out
- Making tables
- Making assumptions
- Guessing and checking
- Using equations
This helps students think logically and tackle other math problems strategically.
How to solve Chicken-and-Rabbit problems?
Our Spark Math teachers have summed up four effective methods—solving by drawing, making a table, making assumptions, and using equations to solve the chicken-and-rabbit problem. Each of the methods has its unique advantages.
1. Solving by Drawing
Great for visual learners! Your child can draw circles or ovals for animals, and then add legs to represent the problem. This works well for younger children but can get slower with bigger numbers.
Question:
| There are 4 animals and 10 legs altogether. Chickens have 2 legs, and rabbits have 4 legs. How many chickens and how many rabbits are there? |
Step-by-step procedure:
- Draw 4 ovals to represent the 4 animals.
- Next to each oval, draw legs: 2 legs for chickens and 4 legs for rabbits.
- Keep adjusting the legs until the total number of legs equals 10.
- Count the number of chickens and rabbits.
Solution:
First, draw 4 ovals to represent the 4 animals.

Then, we assume all are chickens by adding two legs to each oval.

We’ll only have 8 legs, and 2 more legs are needed to add on. Keep adjusting the drawing until the total number of legs equals 10.

Finally, we can count the number of chickens (ovals with 2 legs) and rabbits (ovals with 4 legs).
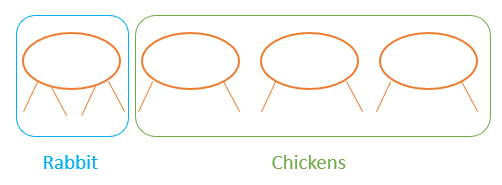
Therefore, there are 3 chickens and 1 rabbit.
2. Make a Table
The next method helps logical thinkers see patterns. Get your child to make a table listing all possibilities for chickens and rabbits. Then, calculate the total legs for each option.
While this helps children look for patterns and logical connections, it can be tedious with many options especially when the problem involves bigger numbers.
Question:
| There are 10 animals and 28 legs altogether. Chickens have 2 legs, and rabbits have 4 legs. How many chickens and how many rabbits are there? |
Step-by-step procedure:
- We can begin with 10 chickens and 0 rabbits.
2. Reduce the number of rabbits by 1. At the same time, increase the number of chickens by 1.
3. Look at the row where the total number of legs is 28 for the final answer.
Solution:
| No. of chickens (2 legs each) | No. of rabbits (4 legs each) | Total animals | Total legs |
|---|---|---|---|
| 10 | 0 | 10 | 10 × 2 = 20 |
| 9 | 1 | 10 | 9 × 2 + 1 × 4 = 22 |
| 8 | 2 | 10 | 8 × 2 + 2 × 4 = 24 |
| 7 | 3 | 10 | 7 × 2 + 3 × 4 = 26 |
| 6 | 4 | 10 | 6 × 2 + 3 × 4 = 28 |
Therefore, there are 6 chickens and 4 rabbits.
3. Making Assumptions
This method encourages critical thinking because your child gets to guess the number of chickens, calculate the legs, and adjust based on the difference from the actual total.
It’s fast if the guess is right. However, it is much less structured and heavily reliant on making good guesses or estimations at the start.
Question:
| A farmer has 11 chickens and rabbits. These animals have a total of 30 legs. How many chickens does he have? How many rabbits does he have? |
Step-by-step procedures:
- Assume all 11 animals are chickens and find its total number of legs.
- Find out the number of legs that are in excess or shortage.
- Use the difference of leg number between the two animals to find out the actual number of rabbits.
- Use the actual number of rabbits to find out the actual number of chickens.
Solution:
- Assume all 11 animals are chickens.
11 × 2 = 22 legs
However, the total number of legs in the farm is 30.
30 – 22 = 8
Why is there a shortage of 8 legs? It’s because some rabbits are counted as chickens. - Replace some chickens with rabbits so that you have 8 more legs to reach 30.
A chicken has 2 legs, and a rabbit has 4 legs.
4 – 2 = 2
So, the difference in the number of legs is 2. - Calculate the number of rabbits needed.
8 ÷ 2 = 4
So, 4 rabbits are needed. - Replace 4 chickens with 4 rabbits:
11 – 4 = 7
Therefore, the farmer has 4 rabbits and 7 chickens.
4. Using Equations
Using equations is precise, scalable, and reinforces algebra. This is best for older children comfortable with algebra. They set up equations for the total number of animals and total legs, then solve for the number of chickens and rabbits. It’s precise but can be tricky for those weak in algebra.
Question:
| A farmer has 10 chickens and rabbits. These animals have a total of 28 legs. How many chickens does he have? How many rabbits does he have? |
Step-by-step procedures:
- Let C be the number of chickens and R be the number of rabbits.
- Total animals:
C+R=10 - Total legs:
2C+4R=28 - Simplify the legs equation:
C+2R=14 - Subtract the animal equation from the simplified legs equation:
(C+2R)−(C+R) =14−10
R=4
So, there are 4 rabbits. - Substitute R=4 back into the animal equation:
C+4=10
C = 10-4
C=6
Therefore, there are 6 chickens and 4 rabbits.
What is the best method to solve the chicken-and-rabbit problems?
There’s no one-size-fits-all method for solving chicken-and-rabbit problems. In fact, each method has its unique strengths and drawbacks, and can be effective depending on the student’s learning style and the complexity of the problem.
| Method | Best for | Strengths | Drawback |
| Solving by Drawing | Visual learners, younger students | Easy to visualize and understand the problem | Slow, impractical for big numbers |
| Making a Table | Logical and analytical learners | Systematic, spot patterns | Tedious with many options |
| Making Assumptions | Trial and error learners | Quick if correct, encourages critical thinking | Wrong guesses require redoing |
| Using Equations | Older students, algebra learners | Precise, good for complex problems | Abstract, hard for those weak in algebra |
Master all four! At Spark Math, we teach our students all four problem-solving methods so that they can choose the best approach for any challenge! After all, we aim to help students become versatile problem solvers.
Bonus! Free Chicken-and-Rabbit Problems Math Worksheets
Our Spark Math teachers have prepared Chicken-and-Rabbit Problems free worksheets tailored for different learning styles and grade levels. Download and have fun solving the puzzles with your child now!
Lower Primary

Upper Primary

International Math Competition

Check out our Spark Math Competition Programme to see how our Spark Math teachers guide your child on the path to becoming math champions!
Answer Keys:
| Level | Keys |
|---|---|
| Lower Primary | 1. 7 chickens and 5 rabbits. 2. 4 spiders and 6 dragonflies. 3. 4 pens and 2 pencils. |
| Upper Primary | 1. 9 chickens and 8 rabbits. 2. 8 trucks and 6 cars. 3. 5 two-dollar stamps and 6 one-dollar stamps. 4. 4 big boxes and 6 small boxes. 5. 4 science fiction books and 2 comic books. |
| International Math Competition | 1. (C) 139. 2. (C) 5. 3. 63 penguins and 37 polar bears. 4. 40 animal figures. 5. 70 chickens. 6. 25 twenty-cent and 10 fifty-cent stamps. 7. 22 animals. 8. 6/7 |
Subscribe to our Spark Education blog for the latest educational information and Spark Math free worksheets.
How Spark Math Teaches Math?
Spark Math by Spark Education empowers K2-P6 children to build strong numeracy skills, master problem-solving strategies, and excel in Math. We go beyond the Singapore MOE syllabus, preparing students for advanced competition problems and real-world applications of math.
Our live, interactive online classes feature experienced teachers using dual-interface technology, gamification and animation to create a fun and effective learning environment for mastering advanced math concepts. Spark Math provides a complete learning package with both physical and digital resources, including textbooks, workbooks, and math manipulatives.
Our program also allows you to create a personalized learning environment for your child at home, with the convenience of managing their schedules and monitoring progress through our parent app.
Ready to see the difference?
Try our FREE trial class with our Spark Math teachers. Experience firsthand how Spark Math can help your child succeed in Math.




