Today, we’re going to learn some super easy tricks to convert fractions into decimals and decimals back into fractions. These tricks will make math a breeze and help you solve problems quickly. It is essential for primary students to understand fractions and decimals. Equally important is the ability to convert between these two forms. So, this foundational knowledge not only enhances mathematical proficiency but also builds critical problem-solving skills that are vital for future learning.
What is a Fraction?
A fraction represents a part of a whole. It consists of two numbers:
- Numerator: The top number, which tells you how many parts you have.
- Denominator: The bottom number, which tells you how many equal parts the whole is divided into.
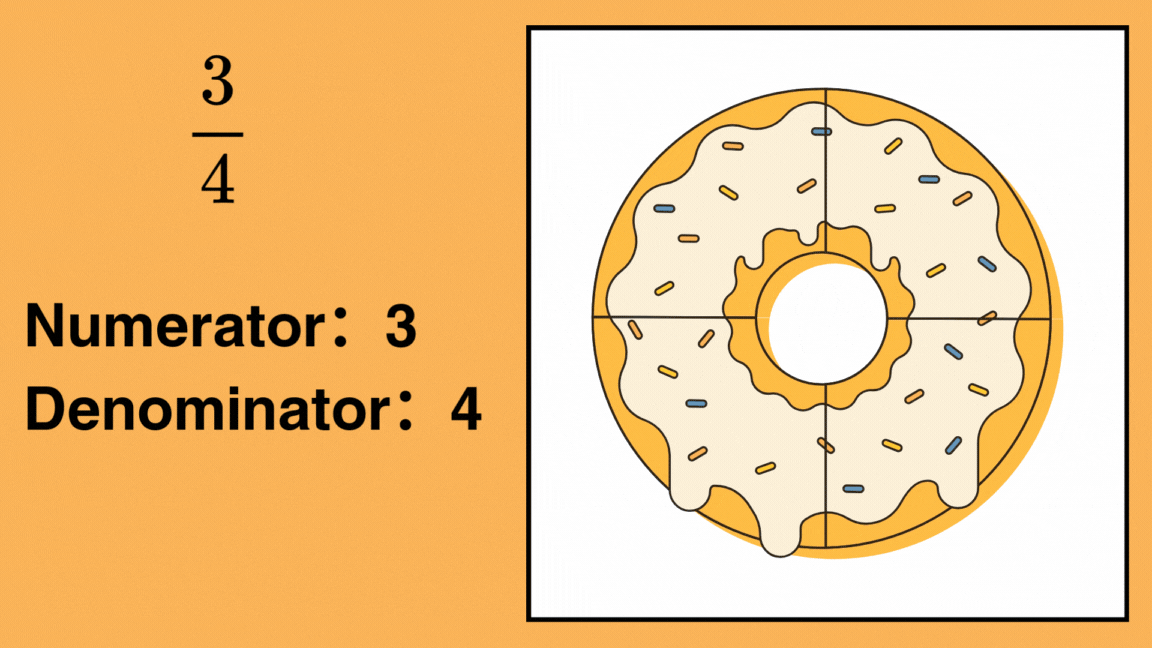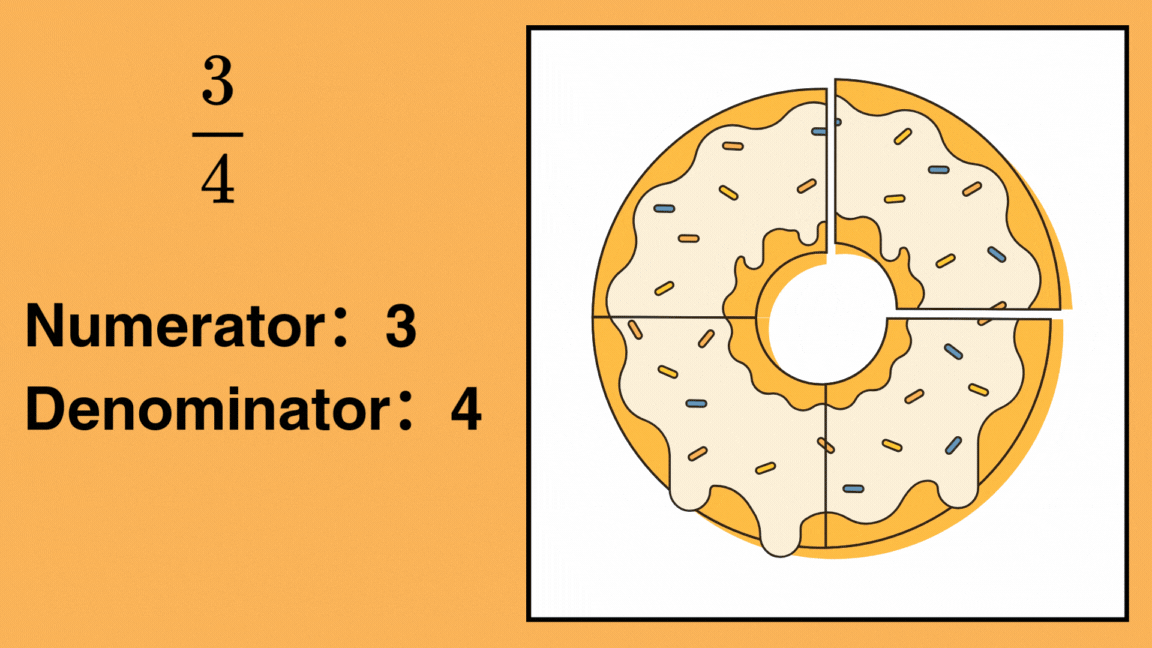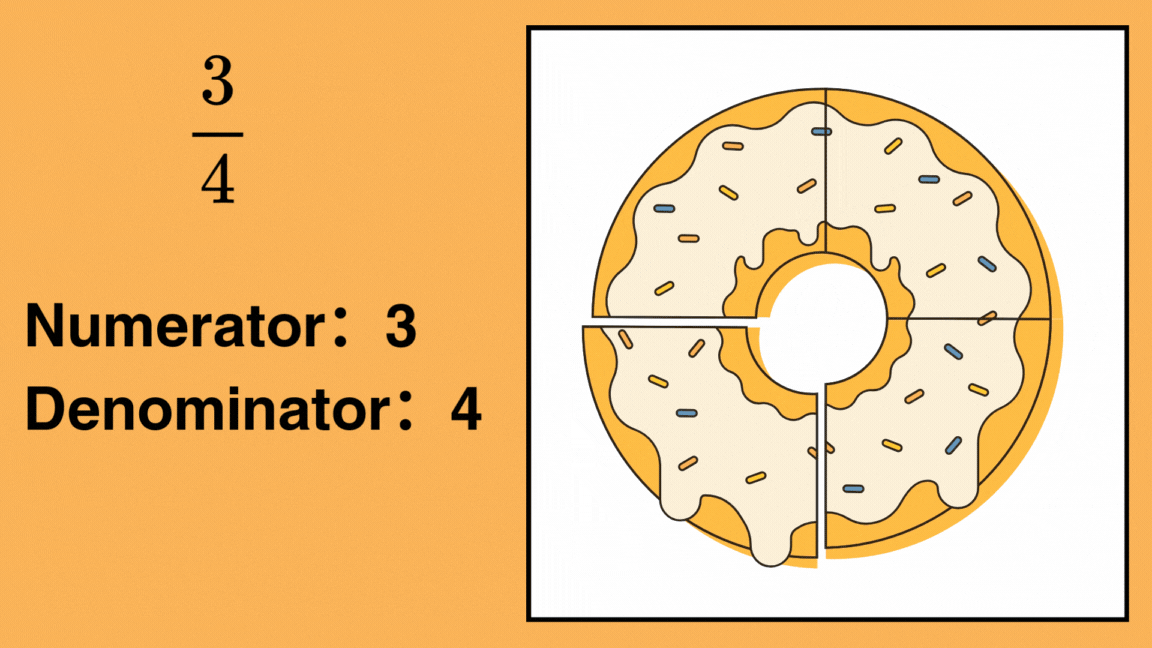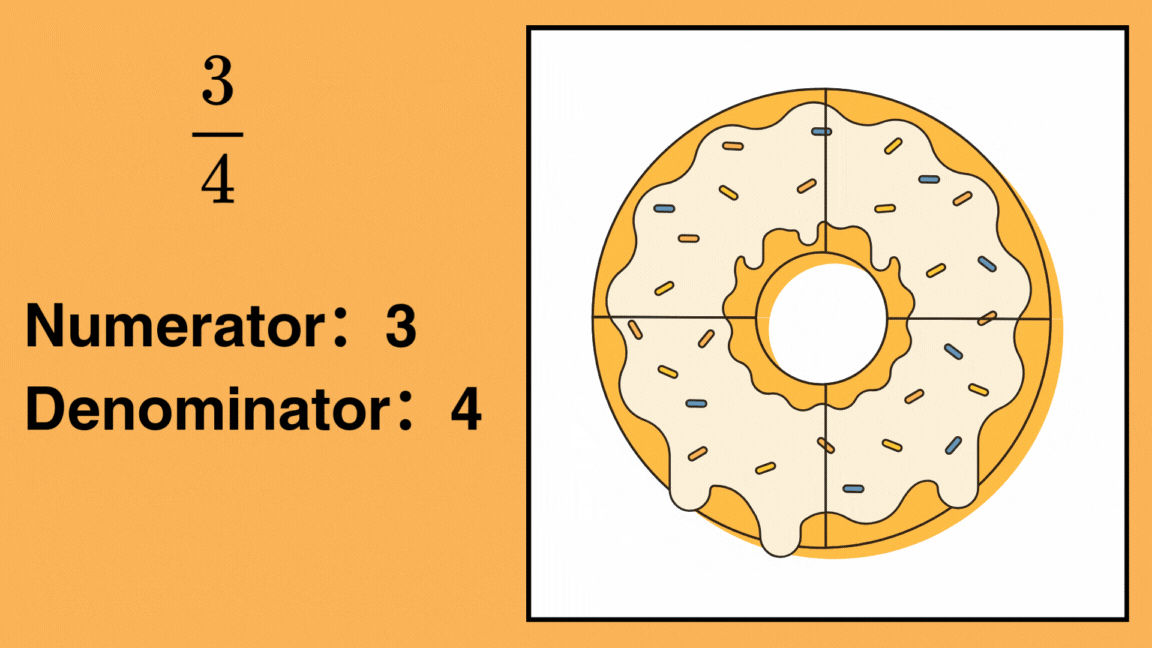
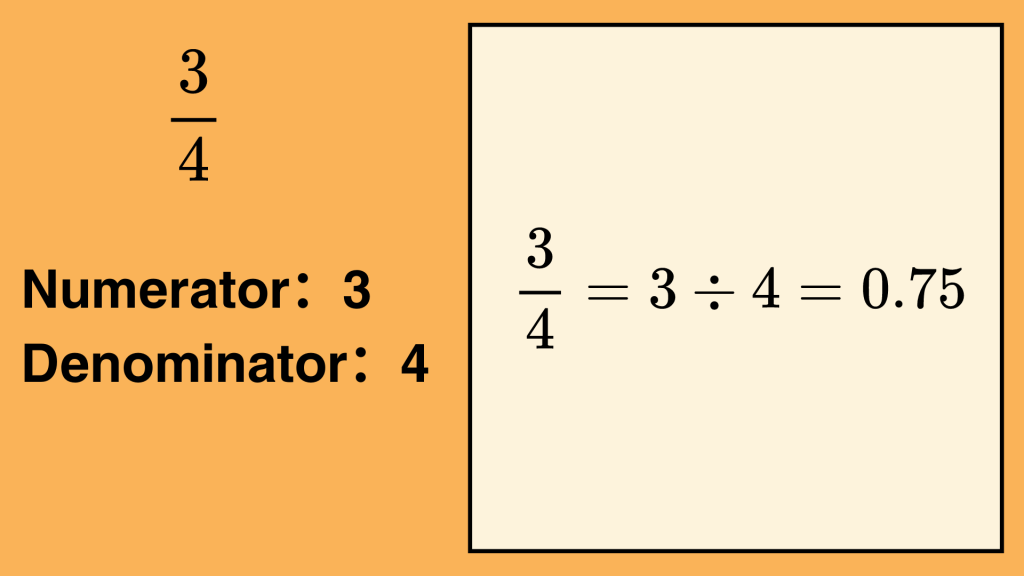
For example, in the fraction
- The numerator is 3, meaning you have 3 parts.
- The denominator is 4, meaning the whole is divided into 4 equal parts.
What is a Decimal?
A decimal is another way to represent fractions or parts of a whole using place value. Decimals use a point (.) to separate the whole number part from the fractional part.
For example, the decimal 0.75 represents 75 hundredths or 75/100.

Converting Fractions to Decimals
To convert a fraction to a decimal, you simply divide the numerator (the top number) by the denominator (the bottom number). Here’s how you can do it:
Step-by-Step Trick:
Set Up the Division: Write the numerator (top number) inside the division bracket and the denominator (bottom number) outside.
Example: To convert
into a decimal, set up 3 ÷ 4.
Divide: Perform the division. If the numerator is smaller than the denominator, you’ll need to add a decimal point and zeros.
Quick Tip:
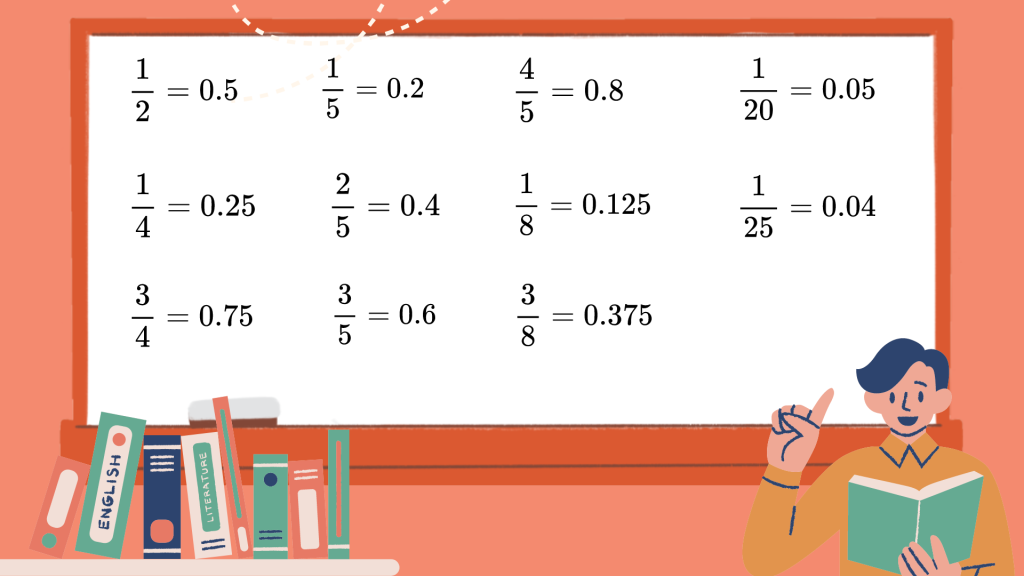
- Common Fractions: Memorize the decimal equivalents of common fractions. This will save you time!
Converting Decimals to Fractions
To convert a decimal to a fraction, follow these simple steps:
Step-by-Step Trick:
Write the Decimal as a Fraction: Place the decimal over its place value. For example, if you have 0.75, write it as
This is because there are two digits after the decimal point.
Simplify the Fraction: Reduce the fraction by finding the greatest common divisor (GCD) of both the numerator and the denominator and dividing both by that number.
Example:

Quick Tip:
Terminating Decimals: If your decimal ends (like 0.5 or 0.25), it’s easier to convert directly as described above.

Repeating Decimals: For repeating decimals like 0.333… (where “3” repeats), write it as a fraction with the repeating part in the numerator over a denominator of nines equal in length to the repeating sequence.
Example:
Practice Makes Perfect
Here are some examples for you to practice:
Convert Fractions to Decimals:
1.
2.
3.
Answers:
1.
2.
3.
Convert Decimals to Fractions:
0.125
0.45
0.9
Answers:
1.
2.
3.




