Mathematics often feels like a puzzle waiting to be solved. Among the various mathematical challenges, two-step equations are a fundamental concept that bridges the gap between basic arithmetic and more advanced algebra. Understanding how to solve these equations is crucial for young learners as they progress in their math education. In this blog post, we’ll break down two-step equations and provide a straightforward strategy for solving them.

What is a Two-Step Equation?

Two-step equations are algebraic problems that can be solved in just two steps. These equations are linear equations involving only one variable. When solving a two-step equation, we perform the same operation on both sides of the equation to simplify it. This helps us to isolate the variable on one side of the equation and find its value. These operations typically involve addition or subtraction, followed by multiplication or division. Here’s what a general two-step equation looks like:

Where:

• a, b, and c are constants (numbers).
• x is the variable we need to solve for.

Why Learn Two-Step Equations?

Foundation for Advanced Math

Two-step equations are a fundamental building block in the world of algebra and beyond. Here’s why:

• Transition to Complex Algebra: Mastering two-step equations prepares students for more complex algebraic concepts, such as multi-step equations, inequalities, and systems of equations.
• Prepares for Higher Education: A solid understanding of two-step equations is crucial for success in high school math courses like Algebra I and II, Geometry, and even Calculus.
• Develops Mathematical Fluency: Working with two-step equations helps students become comfortable with manipulating variables and constants, an essential skill in all areas of mathematics.

Real-World Applications

Two-step equations are not just abstract concepts confined to the classroom; they have practical applications in everyday life. Here are some examples:

• Financial Literacy: Understanding how to solve two-step equations can help in managing budgets, calculating interest rates, and planning savings.
  • Example: If you know the total cost of items and the amount of money you have already spent, you can use a two-step equation to determine how much more you need.
• Cooking and Recipes: Adjusting recipes often requires solving two-step equations to maintain the correct proportions of ingredients.
  • Example: If a recipe calls for 3 cups of flour for every 2 cups of sugar, and you want to make a half batch, you can use a two-step equation to find the new amounts needed.

Critical Thinking

Two-step equations play a significant role in enhancing critical thinking skills. Here’s how:

• Problem-Solving Skills: Solving two-step equations requires breaking down a problem into manageable parts and systematically working through each step. This approach is applicable to many types of problems beyond mathematics.
  • Example: If you’re trying to figure out how long it will take to save up for a new bike given your weekly allowance and current savings, setting up a two-step equation helps break down the problem logically.
• Logical Reasoning: Understanding the relationships between different quantities and how changing one affects the other fosters logical reasoning abilities.
  • Example: If increasing one variable leads to an increase or decrease in another variable (e.g., speed vs. travel time), recognizing this relationship helps make informed decisions.
• Analytical Thinking: Analyzing different ways to approach an equation encourages flexibility in thinking and adaptability when faced with new challenges.
  • Example: There may be multiple methods to solve an equation (e.g., using fractions vs. decimals), understanding these methods allows choosing the most efficient one.

Solving Strategy for Two-Step Equations

The general two steps to solve the two-step equations are:

• Step 1: Addition and subtraction to isolate the variable.
• Step 2: Multiplication or division to determine the value of the variable.

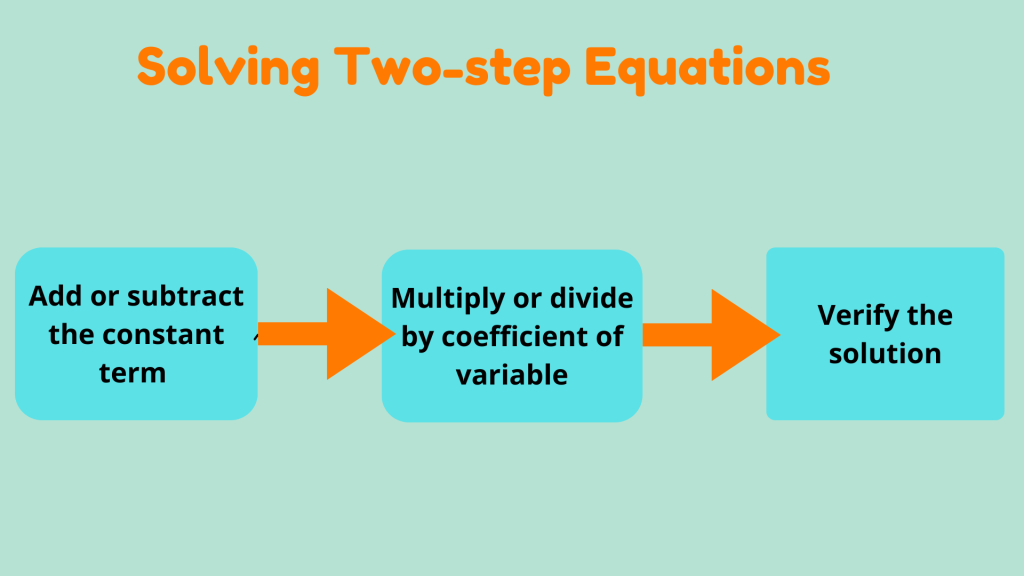
Let’s dive into a simple, step-by-step strategy to solve two-step equations.

Step 1: Isolate the Term with the Variable

The first step is to get rid of the constant term on the same side as the variable. You can do this by performing the opposite operation (addition or subtraction).

For example, consider the equation:

To isolate the term with x, subtract 4 from both sides:

This simplifies to:

Step 2: Solve for the Variable

Next, you need to isolate x by getting rid of the coefficient (the number multiplying x). You can do this by performing the opposite operation (multiplication or division).

Continuing from our previous example:

Divide both sides by 3:

This simplifies to:

And there you have it!

Two Step Equations with Decimals and Fractions

When dealing with decimals, the steps remain the same as with whole numbers, but extra care is needed to handle decimal points correctly. Here are some examples of two-step equations involving both decimals and fractions.

and

When dealing with decimals, the steps remain the same as with whole numbers, but extra care is needed to handle decimal points correctly.

Mastering two-step equations opens door more complex algebraic concepts and real-world problem-solving skills. With simple strategy and regular practice, young mathematicians can confidently tackle these equations and build strong foundation in mathematics.