In geometry, understanding angles and their relationships is crucial. One important relationship is that of consecutive angles. These angles often appear when two lines are intersected by a third line, called a transversal. While consecutive angles are commonly discussed in the context of parallel lines, it’s important to note that this concept applies more broadly to any two lines in the same plane intersected by a transversal. This article will provide a clear explanation of consecutive angles, including both consecutive interior and exterior angles, and discuss important theorems related to these angles.
What Are Consecutive Angles?
Consecutive angles are pairs of angles on the same side of a transversal that intersect two lines. These angles share a common side (the transversal) and are adjacent to each other. It’s important to understand that consecutive angles do not only occur with parallel lines; they can be found whenever two lines are intersected by a transversal within the same plane.
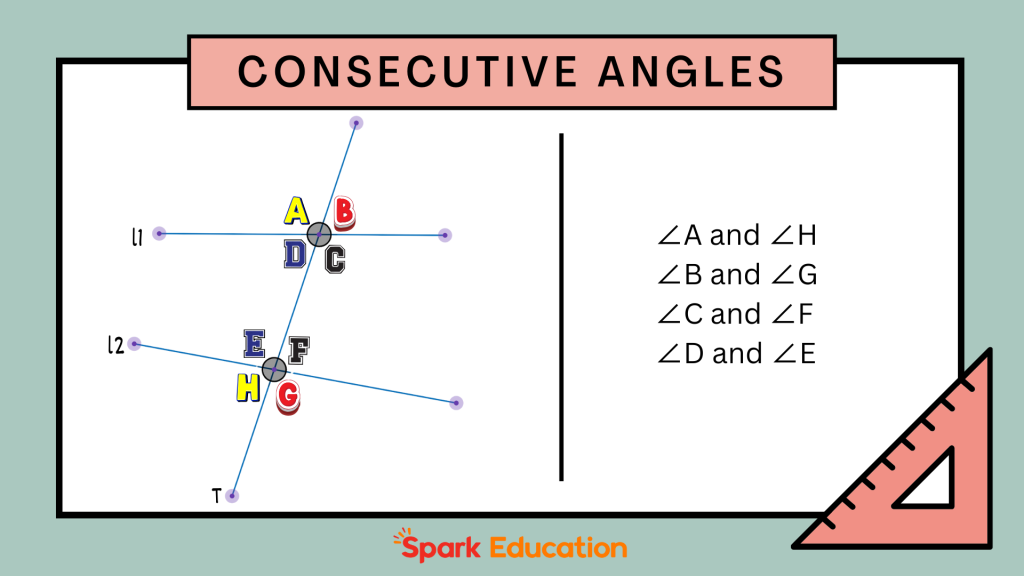
As is shown in the figure above, there are two lines, line L1 and line L2, in a plane, and a transversal line T intersecting both. This intersection creates eight angles (∠A to ∠H). Out of these, the angles that are adjacent and on the same side of the transversal are consecutive angles. In the given figure, the pairs of consecutive exterior angles are:
∠A and ∠H
∠B and ∠G
∠C and ∠F
∠D and ∠E
Types of Consecutive Angles
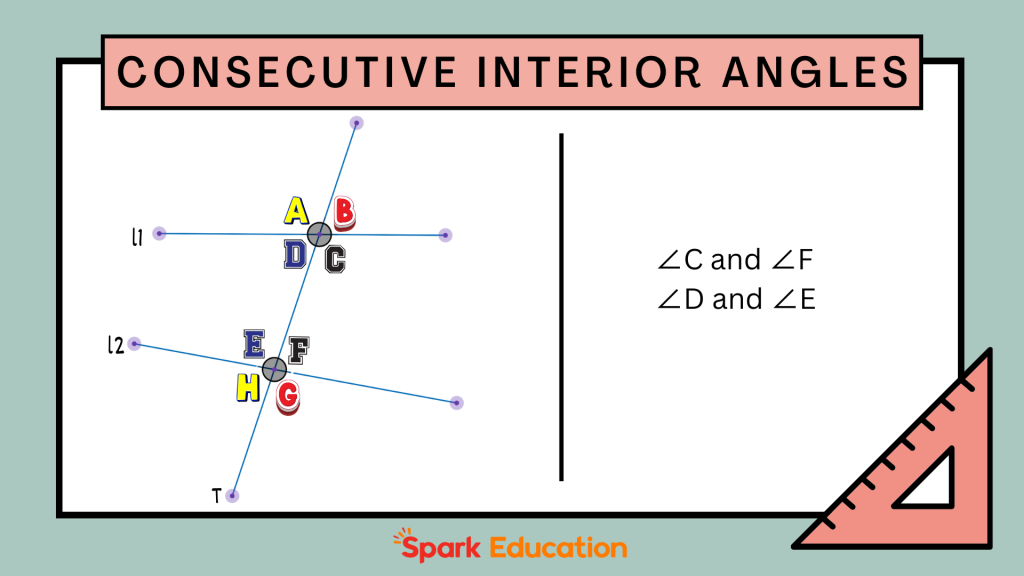
Consecutive Interior Angles
These angles are found between two lines on the same side of the transversal. If the lines are parallel, then consecutive interior angles are supplementary, meaning they add up to 180 degrees.
If two lines L1 and L2 are intersected by a transversal T, angles formed on the inside, like ∠C and ∠F, ∠D and ∠E, are two pairs of consecutive interior angles. Click to view a detailed introduction to consecutive interior angles.
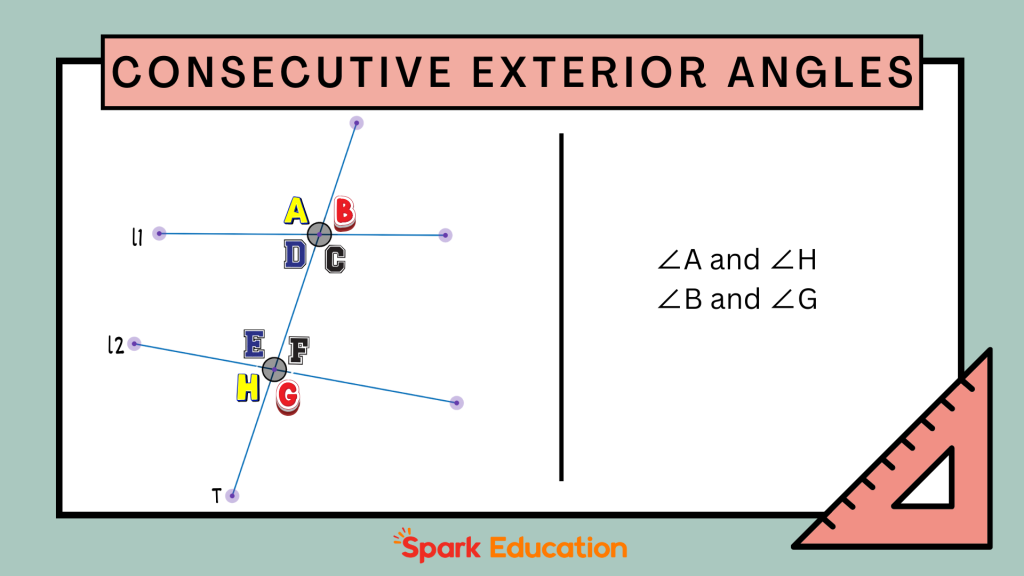
Consecutive Exterior Angles
These are the pairs of angles that are outside the two lines but on the same side of the transversal.
Using the same lines L1 and L2 with transversal T, the angles on the outside, such as ∠A and ∠H, ∠B and ∠G, are two pairs of consecutive exterior angles.
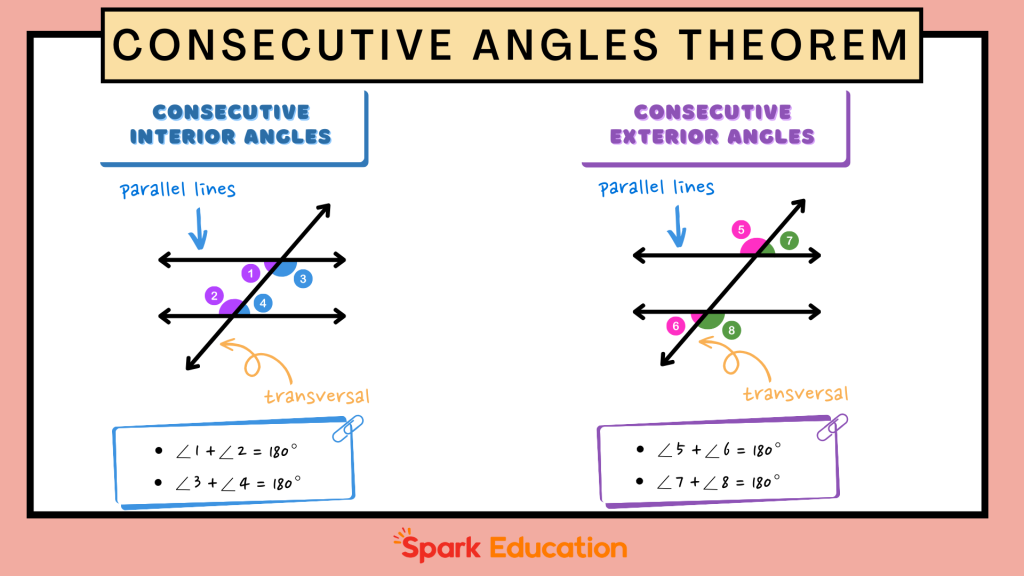
Consecutive Angles Theorem and Its Converse
The Consecutive Angles Theorem states that when two parallel lines are cut by a transversal, both pairs of consecutive interior angles and consecutive exterior angles are supplementary. This means the measures of these angles add up to 180 degrees. This relationship is crucial for understanding how angles interact in parallel line scenarios.
- Consecutive Interior Angles: If two parallel lines are intersected by a transversal, each pair of consecutive interior angles will be supplementary, adding up to 180 degrees.
- Consecutive Exterior Angles: Similarly, for two parallel lines cut by a transversal, each pair of consecutive exterior angles is also supplementary, meaning their measures total 180 degrees.
The Converse of the Consecutive Angles Theorem provides a method for proving that two lines are parallel:
- If two lines are intersected by a transversal such that the consecutive interior angles are supplementary (i.e., their sum is 180 degrees), then the two lines are parallel.
- Likewise, if the consecutive exterior angles formed by the transversal are supplementary, this also proves that the lines are parallel.
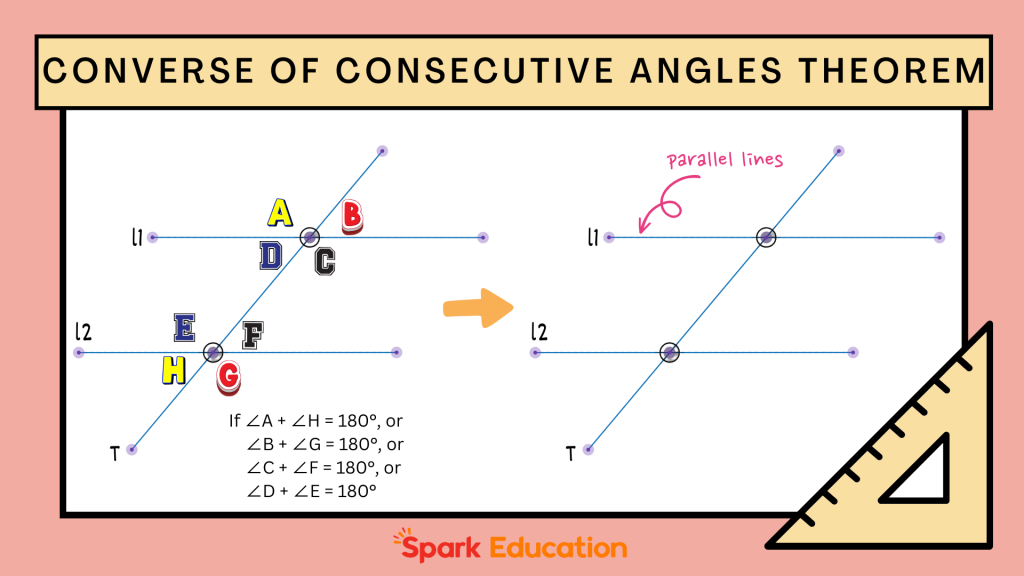
These theorems and their converses are fundamental tools in geometry, allowing us to determine the relationship between lines and angles. They are widely used in geometric proofs and problem-solving to establish whether lines are parallel or to find unknown angle measures.
Consecutive Angles in Parallelograms
In a parallelogram, the opposite sides are parallel. This means that each pair of consecutive angles (angles that share a common side) are supplementary, meaning their measures add up to 180 degrees. This property exists because each pair of consecutive angles in a parallelogram are consecutive interior angles relative to the parallel sides and a transversal line that intersects them.
For example, consider parallelogram ABCD:
- Angle A and Angle B are consecutive angles because they share side AB. Since AB is a transversal intersecting the parallel sides AD and BC, angles A and B are supplementary.
- Similarly, Angle B and Angle C are consecutive and supplementary because they share side BC, with BC acting as a transversal intersecting the parallel sides AB and CD.
Thus, in a parallelogram, any pair of consecutive angles will always sum to 180 degrees. This rule applies to all consecutive angles within the parallelogram:
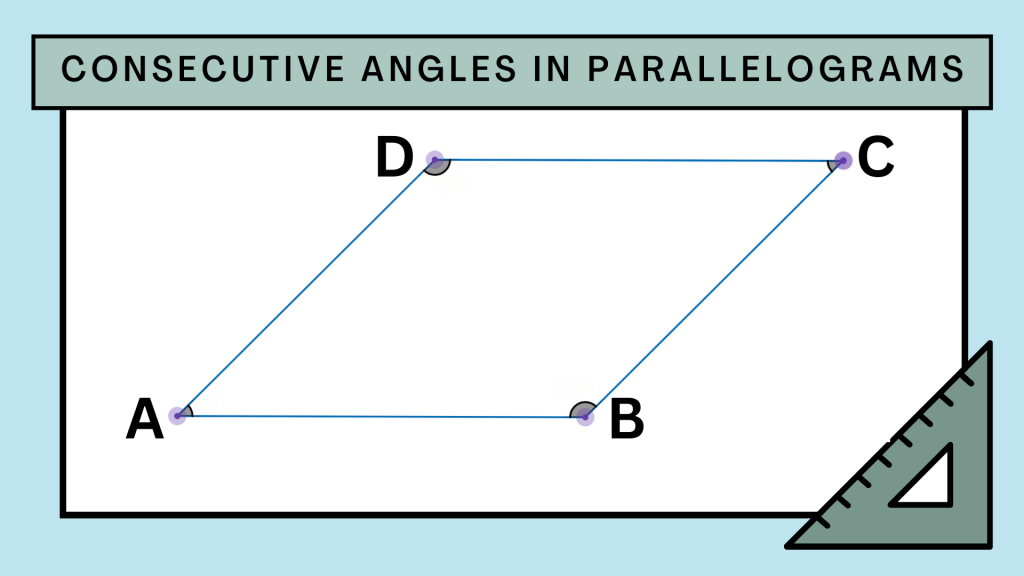
∠A + ∠B = 180°
∠B + ∠C = 180°
∠C + ∠D = 180°
∠D + ∠A = 180°
This property is useful for solving problems involving the angles of a parallelogram and helps in proving certain properties of parallelograms in geometric proofs.
Frequently Asked Questions (FAQ)
1. What are consecutive angles in simple terms?
Consecutive angles are two angles that are next to each other on the same side of a transversal line that intersects two other lines.
2. Do consecutive angles always add up to 180 degrees?
Not necessarily. Consecutive angles are supplementary (add up to 180 degrees) only when the two lines they intersect are parallel.
3. How can we use the consecutive angles theorem to prove lines are parallel?
If you can show that either consecutive interior or exterior angles formed by a transversal are supplementary (add up to 180 degrees), then you can conclude that the two lines being cut by the transversal are parallel.
4. What’s the difference between consecutive interior and exterior angles?
Consecutive interior angles are inside the two lines on the same side of the transversal, while consecutive exterior angles are outside the lines on the same side of the transversal.
Practice Questions
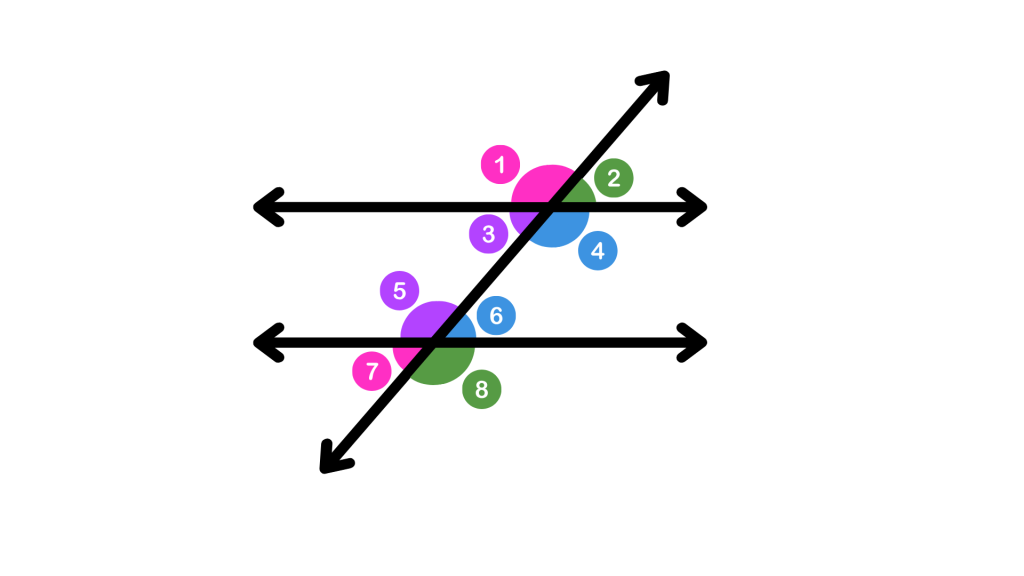
1. Identify Consecutive Interior Angles
Given two lines intersected by a transversal, label the angles formed. Identify one pair of consecutive interior angles.
2. Find the Measure of an Angle
In a parallelogram, one angle measures 75 degrees. What is the measure of its consecutive angle?
3. True or False
If two consecutive interior angles add up to 180 degrees, the lines cut by the transversal are always parallel.
4. True or False
If two consecutive exterior angles add up to 180 degrees, the lines cut by the transversal are parallel.
Answers
1. Angle 3 and angle 5, or angle 4 and angle 6, are consecutive interior angles.
2. Since consecutive angles in a parallelogram are supplementary, the consecutive angle measures 105 degrees (180 – 75 = 105).
3. True, according to the Converse of the Consecutive Interior Angles Theorem.
4. True, this follows from the Converse of the Consecutive Exterior Angles Theorem.
Conclusion
Understanding consecutive angles is essential for mastering geometric concepts and solving related problems accurately. By grasping the definitions, properties, and theorems, along with practicing various problems, you can enhance your proficiency in geometry.
Interested in taking your child’s math skills to the next level? Sign up for a FREE trial class with Spark Math by Spark Education today or try our FREE Online Math Assessment for a detailed report on your child’s math skills! Spark Math is the flagship math course under Spark Education, offering small group classes taught by experienced and engaging real-life teachers. Our program is designed to ignite your child’s passion for learning math, providing a rich array of math resources and an immersive learning experience. Come and see how Spark Math can make a difference in your child’s education!
Related Articles
Everything You Need to Know About Consecutive Interior Angles




