Math, seen as tough, can be made easier for elementary students with visual aids. One such powerful tool is the Venn diagram. Named after the British logician John Venn, these diagrams use overlapping circles to represent relationships between different sets. When introduced at an early age, Venn diagrams can significantly enhance students’ problem-solving skills by simplifying complex concepts and fostering critical thinking.
Venn Diagrams: The Art of Overlapping Sets
Venn diagrams, named after the British logician John Venn, are a staple in the field of mathematics for visualizing relationships between different sets. These diagrams use overlapping circles to represent sets and their intersections, providing a clear and intuitive way to understand complex relationships and solve problems. Their simplicity and effectiveness make them an invaluable tool across various mathematical disciplines, from elementary education to advanced research.
A Venn diagram typically consists of two or more circles that overlap. Each circle represents a set, and the areas where the circles overlap represent the intersection of those sets—elements that are common to both. Areas that do not overlap represent elements that are unique to each set.
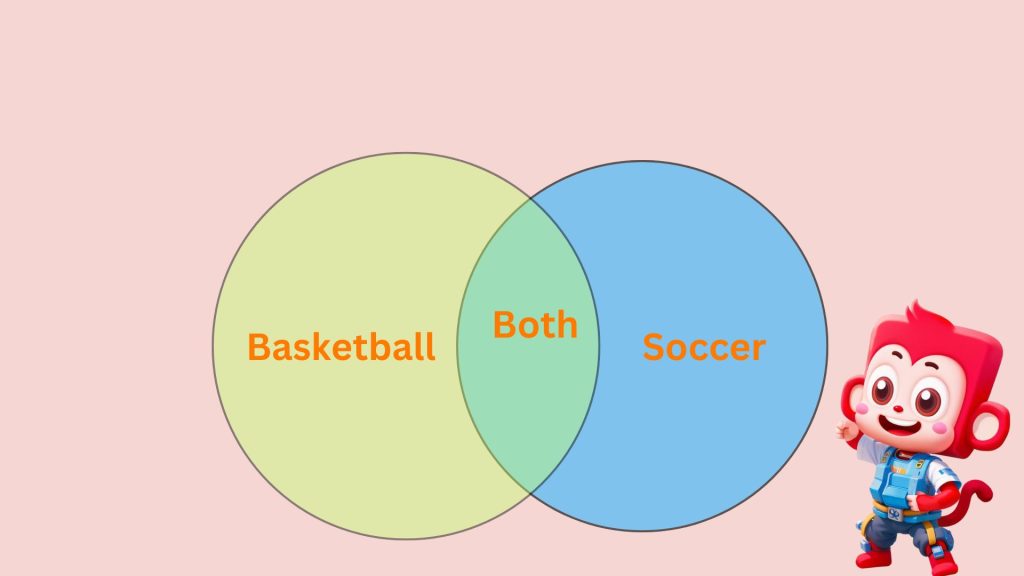
For example, consider two sets: Set A (students who play basketball) and Set B (students who play soccer). The overlapping area would represent students who play both sports. This simple structure allows for easy comparison and analysis of different groups.
Simplifying Complex Concepts
One of the primary benefits of using Venn diagrams in math education is their ability to break down complex problems into simpler, more manageable parts. For young learners who are just beginning to grapple with abstract mathematical concepts, this visual representation can be invaluable.
For example, consider a problem where students are asked to identify common and unique characteristics of two different shapes, such as squares and triangles. By placing the characteristics of squares in one circle and those of triangles in another, students can easily see where the circles overlap—representing shared attributes like both being polygons. This visual separation helps students understand not only what makes each shape unique but also what they have in common.
Enhancing Problem-Solving and Logical Reasoning
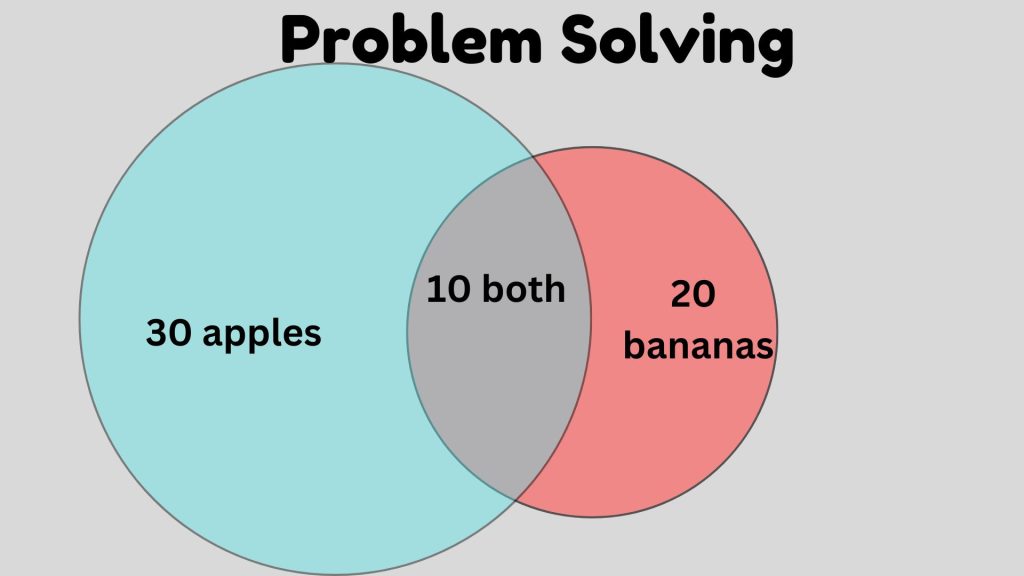
Venn diagrams are powerful tools for problem-solving and logical reasoning. They provide a structured way to approach problems involving multiple sets or conditions. For example, consider a problem where students need to determine how many people have specific preferences:
- 30 people like apples.
- 20 people like bananas.
- 10 people like both apples and bananas.
Using a Venn diagram, students can place these numbers into appropriate sections of overlapping circles representing apple-likers and banana-likers. This visualization helps them easily calculate how many people like only apples or only bananas by subtracting the intersection from the individual totals.
Promoting Critical Thinking
Venn diagrams also promote critical thinking by challenging students to analyze relationships between different sets of data. This analytical skill is crucial for solving more complex mathematical problems as they progress through their education.
Consider a word problem where students must determine which fruits belong in multiple categories: fruits that are red, fruits that are round, and fruits that are both. By using a three-circle Venn diagram, students can visually map out which fruits fit into each category and where they overlap. This method encourages them to think critically about how different attributes intersect, ultimately leading them to a solution.
Encouraging Collaborative Learning
Another advantage of using Venn diagrams in primary math education is their potential to foster collaborative learning. Group activities involving Venn diagrams encourage students to discuss their reasoning with peers, share ideas, and arrive at conclusions collectively.
For example, teachers might assign small groups the task of sorting various objects—such as toys or classroom supplies—into categories using a Venn diagram. Each group member can contribute their thoughts on where an item belongs, promoting discussion and teamwork. This collaborative approach not only enhances understanding but also builds communication skills essential for future academic success.

Ultimately, the use of Venn diagrams transforms abstract mathematical ideas into concrete visual representations, making math more accessible and enjoyable for primary students. As they grow more comfortable with these tools, young learners develop confidence in their problem-solving abilities—a crucial step toward becoming proficient mathematicians and lifelong learners.




