Have you ever been stumped by your child’s questions about math symbols? Those symbols of plus (+), minus (-), multiplication (×) and division (÷) can seem like a mysterious code to young learners.
Let’s explore the origin of these math symbols so you can confidently answer their questions and maybe even inspire a love for math!
Why We Use Math Symbols
Math symbols give us a quick and clear way to represent mathematical concepts.
In the past, mathematicians had to write out operations in full sentences: one plus one equals two. This was tedious and time-consuming. Over time, they created symbols to save time and space.
For example, instead of writing:
“If the length of a rectangle is 5 meters and the width is 3 meters, to find the total area, we would multiply the length by the width.”
You can simply write with symbols:
“Area of rectangle = 5 meters × 3 meters.”
Math symbols help us express mathematical ideas quickly and clearly.
Who Invented Math Symbols
The fact that all Mathematics is Symbolic Logic is one of the greatest discoveries of our age.”
Bertrand Russell, The Principles of Mathematics
Math symbols have fascinating histories! Let’s look at how the symbols for the four basic math operations—addition, subtraction, multiplication, and division—came to be. But first, the “equals to” sign!
Equal-To (=)
| In 1557, Robert Recorde got tired of writing “equals” when teaching algebra. So, he used two lines (=) to represent things are equal. |

In 1557, Robert Recorde, a Welsh mathematician, was writing to teach English students algebra. He grew tired of repeating “is equal to” and decided to use two parallel horizontal lines to represent it.
Robert Recorde introduced the “equals to” symbol in his book The Whetstone of Witte to avoid tedious repetition.
He chose two parallel lines because, to him, nothing could be more equal than parallel lines. He could even have used four-line components or vertical lines.
Fun fact: His book is also acknowledged as the first English book to use the plus and minus signs!
Plus (+) and Minus (-)
| The + and – symbols come from Latin words! “Plus” means “more” and “minus” means “less.” The + symbol comes from the word “et” which means “and” in Latin. |

Today, the plus (+) and minus (-) symbols are universally used for addition and subtraction. The words come from Latin: “plus” means “more” and “minus” means “less.” But where did these symbols come from?
The + and – symbols can trace their roots back to the 14th and 15th centuries. The + sign comes from the Latin word “et,” meaning “and.” Nicole Oresme, a French philosopher, used it to save space in his work, Algorismus Proportionum.
However, the + sign wasn’t always used for addition in the 14th century. In Europe, Luca Pacioli used p̄ for plus and m̄ for minus in early 15th century.
The Egyptian hieroglyph for addition looked like a pair of legs walking in the direction of the text (which could be right-to-left or left-to-right). The reverse symbol was used for subtraction.

On the other hand, the origin of the – symbol is less clear. Some think it came from a tilde (~) used for subtraction.
The + and – signs became popular after Johannes Widmann used them in his book Mercantile Arithmetic. Widmann used + to mean surplus and – to mean deficit.
Multiplication (×)
| This multiplication symbol looks like an “x” but it’s called the “cross of Saint Andrew.” William Oughtred brought it to math world in the 16th century. |

The multiplication symbol (×) might look like a lowercase “x,” but it’s actually called the “cross of Saint Andrew.” An Englishman named William Oughtred gets the credit for bringing this symbol into the math world in the 16th century.
An early use of the × symbol for multiplication can be found in an appendix to Edward Wright’s translation of John Napier’s A Description of the Admirable Table of Logarithmes in 1618. The symbol gained popularity after Oughtred used it in his work Clavis Mathematicae in 1631.
However, German mathematician Gottfried W. Leibniz did not like using × for multiplication, as it could be mistaken for x. He preferred a dot (·) to indicate multiplication, which is now widely used in certain fields.
Division (÷ and /)
| The symbol (÷) was first used by Swiss mathematician Johann Rahn. |
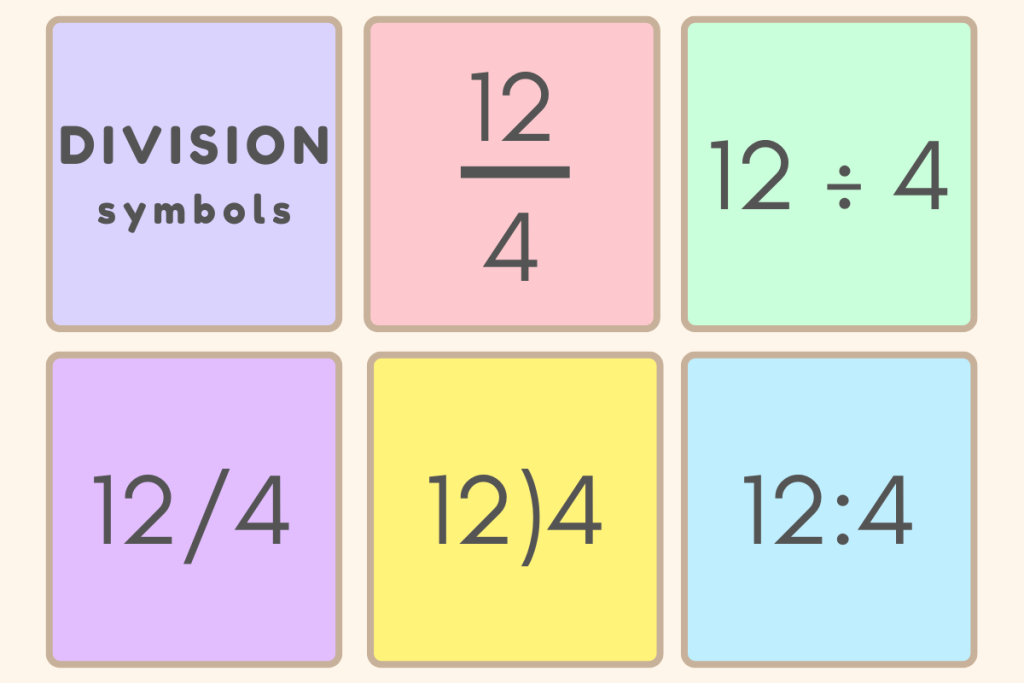
Division symbols have a varied history.
The horizontal fraction bar (—) was introduced by Arab mathematicians and first used in Europe by Fibonacci in the 13th century, but it became popular only in the 16th century.
The obelus (÷), featuring a horizontal bar with a dot above and below, was first introduced by Swiss mathematician Johann Rahn in 1659. While it didn’t gain much traction in Switzerland, it became popular in Britain and the United States and is still commonly used on calculators for division.
The slanted fraction bar (/), introduced by De Morgan in 1845, allowed fractions to be written on a single line, which is the format we use today for division.
Another less common symbol was the parenthesis, which would show 12 divided by 4 as 12) 4 (3).
Gottfried W. Leibniz introduced the colon ( : ) for division, which is still widely used because it keeps division on the same line and connects clearly with multiplication, which he represented with a dot.
Although the obelus (÷) is still commonly used in elementary math, ISO standards now favor the slanted fraction bar (/) for division and the colon (:) for ratios.
The Value of Symbols
With symbols, mathematical calculations would be a manageable mess. They shorten lengthy calculations into smaller terms that are easier to manipulate. Understanding symbols is like learning a language – it takes memorization and practice. Some characters communicate meaning through their form, while others are arbitrary.
So, the next time your child groan at a math problem, remember—those symbols are there for a reason! They’re the result of centuries of mathematicians trying to save time and make things a little less… wordy.
Why limit your knowledge at math symbol trivia? Sign up for a FREE Trial Class with Spark Math by Spark Education or try our FREE Online Math Assessment for a detailed report on your child’s math skills!
Spark Math is a one-of-its-kind online math program. Taught by experienced teachers in small groups with interactive courseware and relatable real-life examples, Spark Math helps kids understand abstract concepts and internalize the problem-solving process. Based on the award-winning Singapore Math curriculum and aligning to international standards, Spark Math helps kids truly understand — and love — math.




