As students enter primary school, they will be introduced to calculations involving 2-digit numbers. Learning some quick calculation tricks can help them master these calculations and build confidence in math. Mathematics often presents itself as a complex subject for many students, but with the right strategies, it can become much more approachable and even enjoyable. One such strategy is “making ten,” a technique that simplifies addition by breaking down numbers into more manageable parts. This method is particularly effective when dealing with 2-digit numbers. Let’s delve into how the “making ten” strategy works and explore its application in adding 2-digit numbers.

What is the “Making Ten” Strategy?

The “making ten” strategy involves decomposing numbers to create sums that are multiples of ten. By doing so, calculations become easier to manage mentally. For instance, when adding single-digit numbers like 8 + 5, one can break it down into 8 + 2 + 3. First, you add 8 and 2 to make ten, and then add the remaining 3 to get the final sum of 13.

Tools to Enhance Understanding of the Strategy

Ten Chart

You may use this ten chart to help students better understand the making ten strategy.

Ten Frame

A ten frame is a simple yet powerful visual tool used in early mathematics education. It consists of a rectangular grid with two rows of five squares each, making a total of ten squares. The primary purpose of a ten frame is to help students visualize numbers and their relationships to ten. By filling in the squares with counters or other markers, students can easily see how numbers are composed and decomposed.

Example:

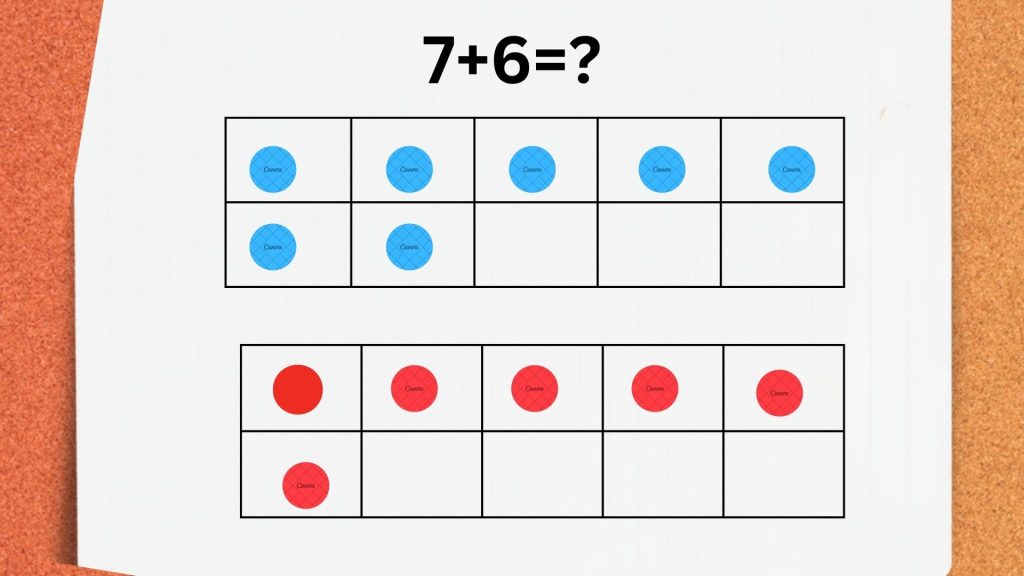
Suppose we have to add the numbers 7 and 6.

In simple words, we have to evaluate 7 + 6.

Draw two ten frames.

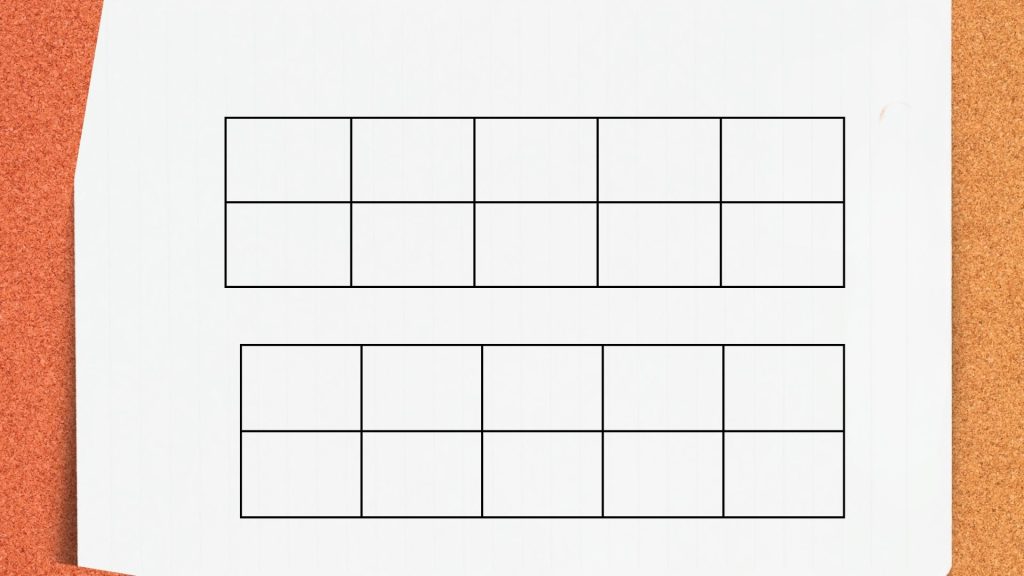
Place 7 chips in the first ten-frame and 6 chips in the second ten-frame. We get:

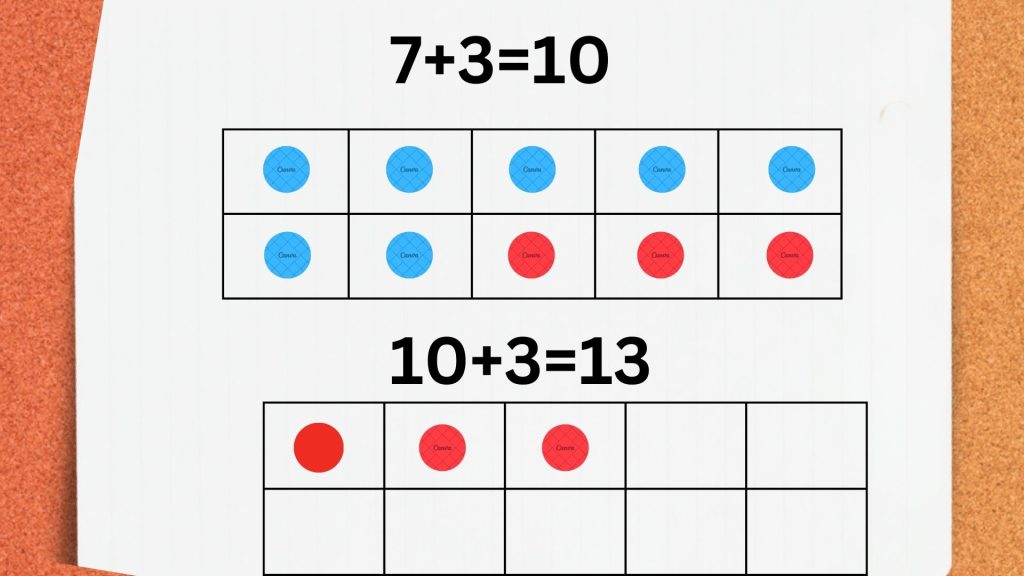
In the top ten-frame, 3 boxes are empty. So, we will take 3 chips from the bottom ten frame and will put them in the top ten frame. This will fill the first frame completely. In the second frame, there are 3 chips.

We write this as

7 + 6 = (7 + 3) + 3 = 10 + 3 = 13

Applying the Strategy to 2-Digit Numbers

When it comes to adding 2-digit numbers, the “making ten” strategy can be extended by focusing on both tens and units separately.

Addition

Step-by-Step Example: Adding 47 and 36

1. Separate Tens and Units:
   1. Break down each number into tens and units.
      • 47=40+7
      • 36=30+6
2. Add Tens Separately:
   1. Add the tens from both numbers.
      • 40+30=70
3. Make Ten with Units:
   1. Look at the units (7 and 6) and figure out how to make ten.
      • 7+3=10, leaving an extra 3 from 6 (since 6=3+3)
4. Combine Results:
   1. Add the results from steps two and three.
      • 70(tens sum)+10(units making ten)=80
   2. Add the remaining unit part.
      • 80+3=83

Thus, 47+36=83.

Subtraction

Step-by-Step Example: Subtracting 47 from 83

1. Separate Tens and Units:
   1. Break down each number into tens and units.
      • 83=80+3
      • 47=40+7
2. Subtract Tens Separately:
   1. Subtract the tens from each other.
      • 80−40=40
3. Make Ten with Units:
   1. Look at the units (3 and 7) and figure out how to make ten.
      • Since we can’t subtract 7 from 3 directly, we need to adjust by borrowing from the tens place.
      • Borrowing one ten from 40, we get 30+13.
4. Combine Results:
   1. Now subtract the units:
      • 13−7=6
   2. Add back the adjusted tens:
      • 30+6=36

Thus, 83−47=36.

Benefits of Using “Making Ten”

Mental Math Efficiency:

By breaking down complex problems into simpler parts, students can perform calculations more quickly in their heads.

Foundation for Future Math Skills:

Mastering this strategy lays a solid groundwork for understanding more advanced mathematical concepts such as algebra.

Increased Confidence:

As students become proficient with this method, their confidence in handling arithmetic operations grows.

Enhanced Number Sense:

This strategy helps students develop a better understanding of number relationships and place value.