Ever wondered how architects design intricate floor plans or artists create captivating mosaic patterns? The secret lies in understanding the art of combining simple shapes to construct complex forms, a concept known as the area of composite figures, which is also a fundamental skill in geometry. This article simplifies the principle of finding the area of composite figures, breaking it down into manageable steps suitable for primary students.
What is a Composite Figure?
A composite figure, also known as a compound or complex shape, is composed of two or more simple geometric shapes. Imagine a world where shapes are like building blocks, waiting to be assembled into masterpieces. A composite figure is precisely that – a union of basic geometric shapes, such as triangles, rectangles, squares, and circles, cleverly arranged to create a larger, more intricate design. These compound shapes can be found all around us, from the architectural marvels that grace our skylines to the mesmerizing patterns adorning our floors and walls.

How to Calculate the Area of Composite Figures
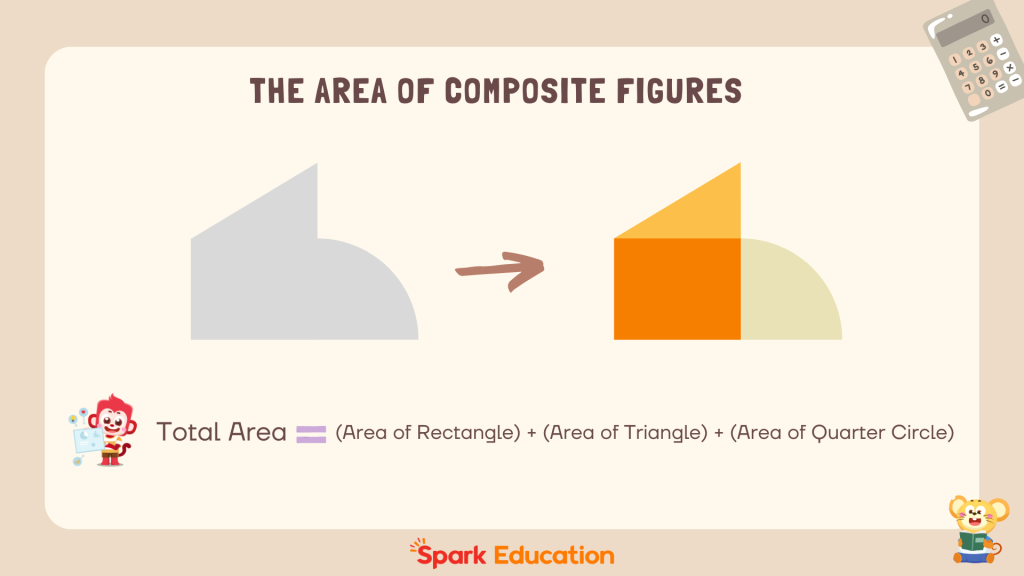
Computing the area of a composite figure requires breaking it down into its simpler components. Here’s a step-by-step process:
Step 1: Identify the Simple Shapes
Examine the composite figure and determine the individual shapes it comprises. For example, the composite shape given in the first picture includes a square, a right triangle and a quarter circle.
Step 2: Calculate the Area of Each Simple Shape
Using standard formulas for area calculation, find the area of each simple shape:
- Rectangle: Area = length × width
- Triangle: Area = 1/2 × base × height
- Quarter Circle: Area = 1/4 × π × (radius)^2
Step 3: Sum Up the Areas
Add the areas of all the simple shapes to get the total area of the composite figure.

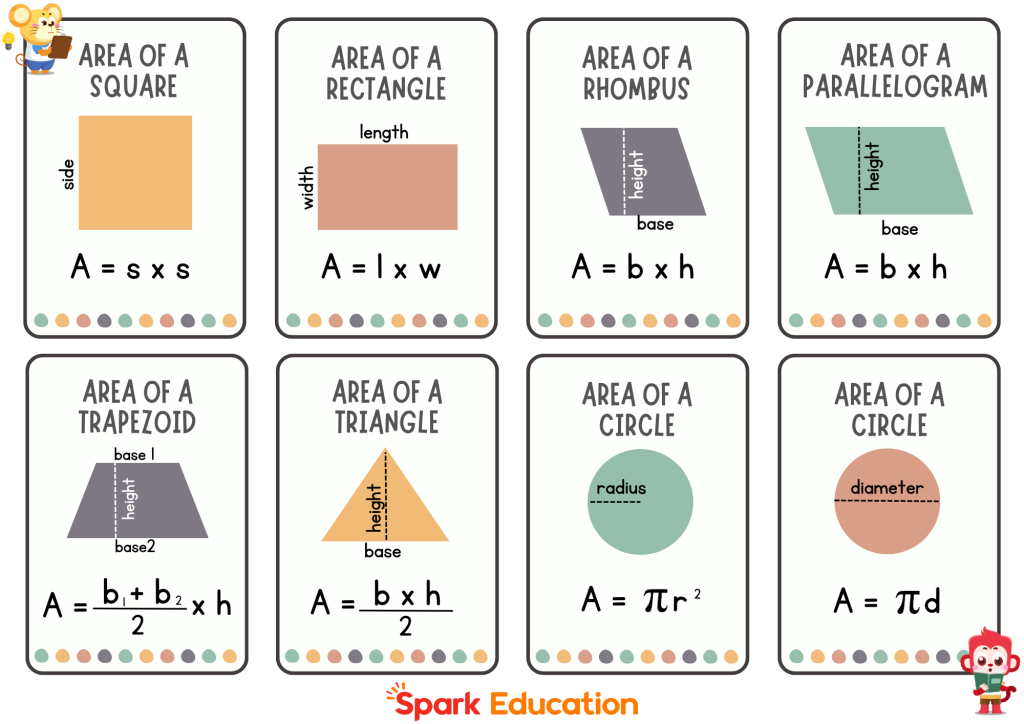
Here is a list of the area formulas for basic shapes:
Practice Problems and Solutions
Problem 1: Find the area of the composite shape below
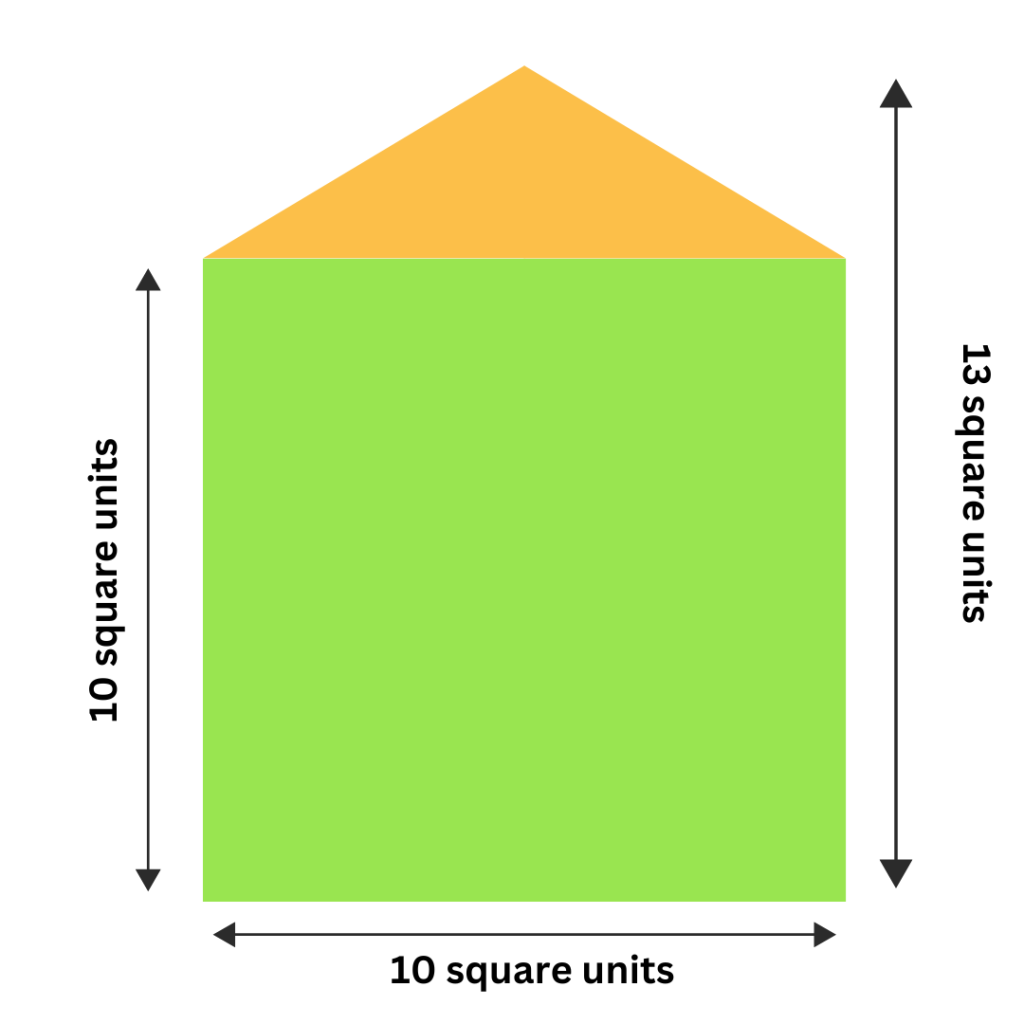
Solution:
- Area of the square: 10^2 = 100 square units.
- Area of the triangle: 1/2 × 10 × (13 – 10) = 1/2 × 10 × 3 = 15 square units.
- Total Area: 100 + 15 = 115 square units.
Problem 2: A composite shape consists of a square and a right triangle with a total area of 200 square units. If the square’s area is 100 square units, find the triangle’s area.
Solution:
- Area of the triangle: 200 − 100 = 100 square units.
FAQs
How do you determine the area of composite figures?
To calculate the area of composite or irregularly shaped figures, start by breaking them down into simpler, non-overlapping shapes. Calculate the area of each of these simpler shapes individually using standard area formulas. Finally, sum up these areas to get the total area of the composite figure.
What are the steps to compute the area of composite shapes?
- Break down the composite shape into basic geometric shapes.
- Calculate the area of each basic shape separately.
- Sum the areas of all the basic shapes to obtain the total area of the composite shape.
What does it mean to decompose a composite figure?
Decomposing a composite figure involves breaking it down into two or more simpler, non-overlapping shapes. This process simplifies the calculation of the figure’s area or for analyzing its components.
Conclusion
Understanding how to calculate the area of composite figures is a valuable skill in both academic and real-world contexts. By breaking down complex figures into simpler shapes and summing their individual areas, we can accurately determine the total area. Keep practicing with different composite shapes to enhance your skills.
Interested in taking your child’s math skills to the next level? Enroll in our FREE Spark Math trial class today! Spark Math is the flagship math course under Spark Education, offering small group classes taught by experienced and engaging real-life teachers. Our program is designed to ignite your child’s passion for learning math, providing a rich array of math resources and an immersive learning experience. Come and see how Spark Math can make a difference in your child’s education!




